Simon Veitner

I’m Simon and 31 years old. I’m into all kinds of stuff related to computing and data science.

9 minute read

The attention module is the key ingredient of what makes up a transformer layer. In this blogpost we will show how to implement it from scratch in JAX alongside with some tricks to enhance performance and efficency.

Let’s consider the two sentences:

  • I swam across the river to get to the other bank
  • I walked across the road to get cash from the bank

Clearly the different meaning of bank in each sentence is clear to us as humans. A neural network should attend to previous words in the sentence to infer the meaning of bank in each of the two sentences.

In the first sentence words like swam and river determine the meaning of bank whereas in the second sentence the word cash gives a strong indication of what bank means in the sentence. This is what attention accomplishes as a module in a neural net.

The attention layer takes three matrices as an argument: Q, K and V. Each of these matrices is obtained by multiplying the vector representation X of a sentence with a matrix, for example: Q = X W_Q etc. The matrices W_Q, W_K, W_V are learned during the training process. You may ask yourself if the names Q, K and V are arbitrary and in fact they are not. Q stands for Query, K stands for Key and V stands for Value. Imagine the situation that a user of a streaming service wants to get a suggestion for a new movie based on it’s preferences. We could encode the user preferences (like genres, actors etc.) into a vector q (the query), encode the information about each movie in store into a vector k (the key) and then calculate the similarity between each query with each key and send the user to the movie with the highest similarity v, a vector which encodes the movie. Attention works similary and maybe a diagram helps us best to understand the mechanism:

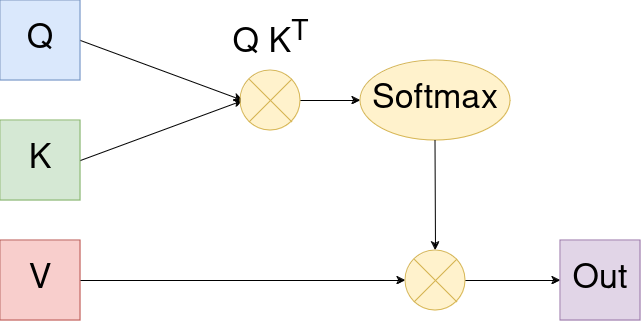
Attention

The shapes of the above matrices are as follows:

  • Q: S x D
  • K: S x D
  • V: S x D_v

In this context S is the number of tokens. For now we can think about it (roughly) as the number of words in the text at hand. Let’s explain the components above: Q K^T: The (i,j) entry of this matrix contains the scalar product, i.e. the similiarity, between the i’th query and the j’th key vector. We then use a softmax to normalize these weights and use them to build the weighted average of values for each part of the sequence. Typicially we use multiple attention heads. That gives us ability to have each head focus on different parts to pay attention to. We then concat the different attention outputs and this is our multi head attention output. Let’s see a how to implement that in code for a batch of examples in JAX. We can compare with the pallas attention available in jax to check for correctness.

import jax
from jax.experimental.pallas.ops import attention as pallas_attention
from timing_util import simple_timeit

BATCH = 128
HEADS = 4
SEQUENCE = 1024
HEAD_DIM = 128

Q = jax.random.normal( jax.random.key(0), (BATCH, SEQUENCE, HEADS, HEAD_DIM))
K = jax.random.normal( jax.random.key(1), (BATCH, SEQUENCE, HEADS, HEAD_DIM))
V = jax.random.normal( jax.random.key(2), (BATCH, SEQUENCE, HEADS, HEAD_DIM))

@jax.jit
def attention_ourselves(_Q, _K, _V):
    _weights_unnormalized = jax.numpy.einsum("BSHD,BTHD->BHST", _Q, _K)
    _weights = jax.nn.softmax(_weights_unnormalized)  
    output = jax.numpy.einsum("BHST,BTHD->BSHD", _weights, _V)

    return output

def attention_pallas(_Q, _K, _V):
    return pallas_attention.mha_reference(_Q, _K, _V,  segment_ids=None, causal=False)

attn_ourselves_value = attention_ourselves(Q,K,V)
attn_value = attention_pallas(Q,K,V)

assert jax.numpy.allclose(attn_ourselves_value, attn_value, atol=1e-1, rtol=1e-1)

time_ourselves = simple_timeit(attention_ourselves, Q, K, V, task="ourselves")   
time_pallas = simple_timeit(attention_pallas, Q, K, V, task="pallas")

"""
Output:

ourselves: average time milliseconds: 8.13, trace /tmp/t_ourselves_9ZMO2723QB
pallas: average time milliseconds: 8.10, trace /tmp/t_pallas_KKX3Q8EF94
"""

This implementation works as expected but it’s missing a component. Causality dictates that what comes next in a sentence is given by what was “said” before. This can be accomedated for by using the following mask, which zeros out components of the weight matrix at each sequence step: 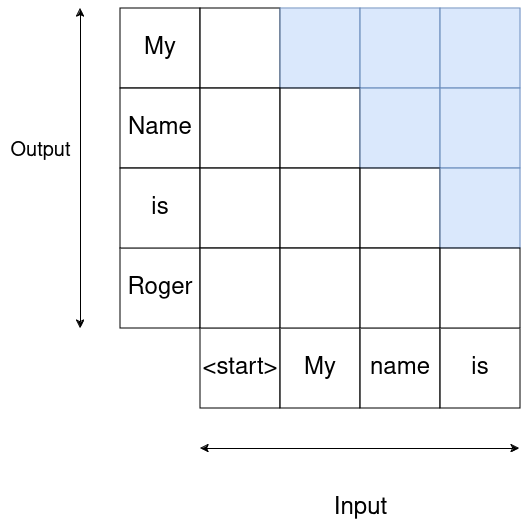Causal Mask That means where we want to predict ìs we only have weight contribution from <start>, My and name. In JAX we can zero out the contribution for “non causal” weights as follows:

import jax
from jax.experimental.pallas.ops import attention as pallas_attention
from timing_util import simple_timeit

BATCH = 128
HEADS = 4
SEQUENCE = 1024
HEAD_DIM = 128

Q = jax.random.normal( jax.random.key(0), (BATCH, SEQUENCE, HEADS, HEAD_DIM))
K = jax.random.normal( jax.random.key(1), (BATCH, SEQUENCE, HEADS, HEAD_DIM))
V = jax.random.normal( jax.random.key(2), (BATCH, SEQUENCE, HEADS, HEAD_DIM))


def get_causal_mask(length, out_shape=None):
    mask = jax.numpy.triu(jax.numpy.ones((length, length)), 1)
    if out_shape is not None:
        ### Add batch and head dimensions
        mask = jax.numpy.expand_dims(mask, 0)
        mask = jax.numpy.expand_dims(mask, 0)
        mask = jax.numpy.broadcast_to(mask, out_shape)
    mask = mask.astype(jax.numpy.bool_)
    return mask

mask_example = get_causal_mask(8)
print(mask_example)

@jax.jit
def attention_ourselves(_Q, _K, _V):
    _weights_unnormalized = jax.numpy.einsum("BSHD,BTHD->BHST", _Q, _K)
    _mask = get_causal_mask(SEQUENCE, _weights_unnormalized.shape)
    _weights = jax.nn.softmax(_weights_unnormalized-1e6*_mask)  
    output = jax.numpy.einsum("BHST,BTHD->BSHD", _weights, _V)

    return output

def attention_pallas(_Q, _K, _V):
    return pallas_attention.mha_reference(_Q, _K, _V,  segment_ids=None, causal=True)

attn_ourselves_value = attention_ourselves(Q,K,V)
attn_value = attention_pallas(Q,K,V)

assert jax.numpy.allclose(attn_ourselves_value, attn_value, atol=1e-1, rtol=1e-1)

time_ourselves = simple_timeit(attention_ourselves, Q, K, V, task="ourselves")   
time_pallas = simple_timeit(attention_pallas, Q, K, V, task="pallas")

"""
Output:

[[False  True  True  True  True  True  True  True]
 [False False  True  True  True  True  True  True]
 [False False False  True  True  True  True  True]
 [False False False False  True  True  True  True]
 [False False False False False  True  True  True]
 [False False False False False False  True  True]
 [False False False False False False False  True]
 [False False False False False False False False]]
ourselves: average time milliseconds: 8.34, trace /tmp/t_ourselves_XVOJXQ6S8W
pallas: average time milliseconds: 8.11, trace /tmp/t_pallas_FVWQ4IAHT2 
"""

There is another optimizaton we can make. Assume we have a bunch of sequences which we want to train on. The maximum sequence length might be a number N. It would be very unlikely that all sequences have exactly this length. In fact we expect most of them to be shorter. This leads to the concept of packing where we might pack multiple sequence into one row. For that to work we need to ensure that the sequences don’t interact. I.e. the different sequences should only pay attention to themselves. Let’s visualize that for the example that we have a sequence length of 8. The first 4 tokens are an own sequence, the next three are an own sequence and the last token is an own sequence:

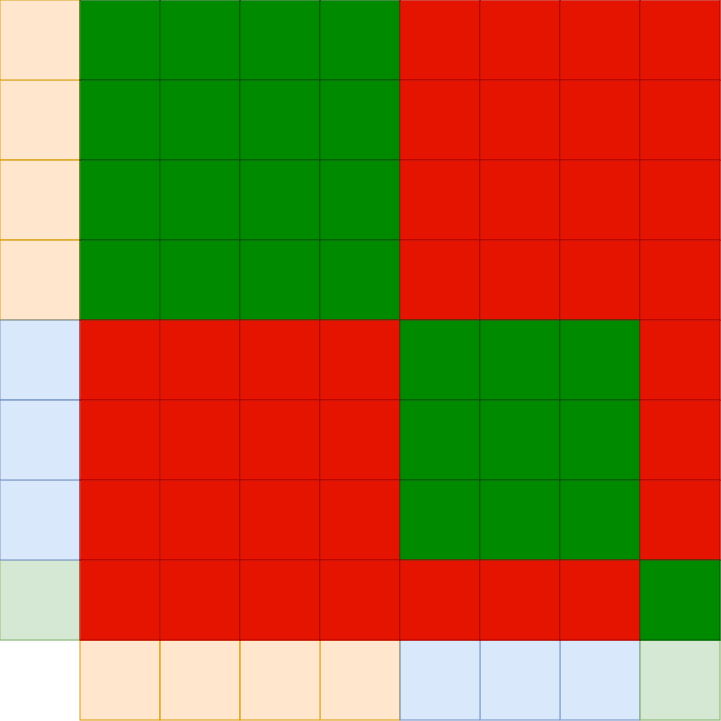Packing Mask The red fields mean “masking out”.

We can accomplish this in JAX as follows:

import jax
from jax.experimental.pallas.ops import attention as pallas_attention
from timing_util import simple_timeit

BATCH = 128
HEADS = 4
SEQUENCE = 1024
HEAD_DIM = 128

Q = jax.random.normal( jax.random.key(0), (BATCH, SEQUENCE, HEADS, HEAD_DIM))
K = jax.random.normal( jax.random.key(1), (BATCH, SEQUENCE, HEADS, HEAD_DIM))
V = jax.random.normal( jax.random.key(2), (BATCH, SEQUENCE, HEADS, HEAD_DIM))

seq0 = jax.numpy.ones((BATCH, SEQUENCE//2))
seq1 = jax.numpy.ones((BATCH, 3 * SEQUENCE//8)) + 1
seq2 = jax.numpy.ones((BATCH, SEQUENCE//8)) + 2
seq_ids = jax.numpy.concatenate([seq0, seq1, seq2], axis=1)

def get_packing_mask(seq_ids, out_shape=None):
    # B x S x 1
    expand0 = jax.numpy.expand_dims(seq_ids, axis=2)
    # B x 1 x T
    expand1 = jax.numpy.expand_dims(seq_ids, axis=1)
    # B x S x T
    mask = ~jax.numpy.equal(expand0, expand1)
    if out_shape is not None:
        ### Add head dimension
        mask = jax.numpy.expand_dims(mask, 1)
        mask = jax.numpy.broadcast_to(mask, out_shape)
    mask = mask.astype(jax.numpy.bool_)
    return mask

seq0_example = jax.numpy.ones((1, 8//2))
seq1_example = jax.numpy.ones((1, 3 * 8//8)) + 1
seq2_example = jax.numpy.ones((1, 8//8)) + 2
seq_ids_example = jax.numpy.concatenate([seq0_example, seq1_example, seq2_example], axis=1)
mask_example = get_packing_mask(seq_ids_example)
print(seq_ids_example)
print(mask_example)

@jax.jit
def attention_ourselves(_Q, _K, _V):
    _weights_unnormalized = jax.numpy.einsum("BSHD,BTHD->BHST", _Q, _K)
    _mask = get_packing_mask(seq_ids, _weights_unnormalized.shape)
    _weights = jax.nn.softmax(_weights_unnormalized - 1e6*_mask)  
    output = jax.numpy.einsum("BHST,BTHD->BSHD", _weights, _V)

    return output

def attention_pallas(_Q, _K, _V):
    return pallas_attention.mha_reference(_Q, _K, _V,  segment_ids=seq_ids, causal=False)

attn_ourselves_value = attention_ourselves(Q,K,V)
attn_value = attention_pallas(Q,K,V)

assert jax.numpy.allclose(attn_ourselves_value, attn_value, atol=1e-1, rtol=1e-1)

time_ourselves = simple_timeit(attention_ourselves, Q, K, V, task="ourselves")   
time_pallas = simple_timeit(attention_pallas, Q, K, V, task="pallas")

"""
Output:

[[1. 1. 1. 1. 2. 2. 2. 3.]]
[[[False False False False  True  True  True  True]
  [False False False False  True  True  True  True]
  [False False False False  True  True  True  True]
  [False False False False  True  True  True  True]
  [ True  True  True  True False False False  True]
  [ True  True  True  True False False False  True]
  [ True  True  True  True False False False  True]
  [ True  True  True  True  True  True  True False]]]
ourselves: average time milliseconds: 9.40, trace /tmp/t_ourselves_DINVH9D3WW
pallas: average time milliseconds: 8.50, trace /tmp/t_pallas_V5NQP4EOMD
"""

We can combine these two masks by using a simple logical OR, i.e. we mask out if condition CAUSAL or condition PACKING demands a mask out.

One more important point is the possibility of parallelizing to leverage multiple chips. In case of attention it turns out that parallelizing is not difficult to reason about.

  • We have BATCH dimension. Each batch is processed independently, so we can always parallelize along this dimension.

  • We have HEADS dimension. By definition each head is independent from the other heads so we can parallelize as well.

The final implementation which uses packing, causality and parallelization looks as follows:

import jax
from jax.experimental.pallas.ops import attention as pallas_attention
from timing_util import simple_timeit
from jax.experimental.mesh_utils import create_device_mesh

BATCH = 128
HEADS = 4
SEQUENCE = 1024
HEAD_DIM = 128

Q = jax.random.normal( jax.random.key(0), (BATCH, SEQUENCE, HEADS, HEAD_DIM))
K = jax.random.normal( jax.random.key(1), (BATCH, SEQUENCE, HEADS, HEAD_DIM))
V = jax.random.normal( jax.random.key(2), (BATCH, SEQUENCE, HEADS, HEAD_DIM))

mesh = jax.sharding.Mesh(create_device_mesh((2,2)), ("x", "y"))
p = jax.sharding.PartitionSpec("x", None, "y", None)
sharding = jax.sharding.NamedSharding(mesh, p)

Q_ = Q
K_ = K
V_ = V

Q = jax.device_put(Q, sharding)
K = jax.device_put(K, sharding)
V = jax.device_put(V, sharding)

seq0 = jax.numpy.ones((BATCH, SEQUENCE//2))
seq1 = jax.numpy.ones((BATCH, 3 * SEQUENCE//8)) + 1
seq2 = jax.numpy.ones((BATCH, SEQUENCE//8)) + 2
seq_ids = jax.numpy.concatenate([seq0, seq1, seq2], axis=1)


def get_causal_mask(length, out_shape=None):
    mask = jax.numpy.triu(jax.numpy.ones((length, length)), 1)
    if out_shape is not None:
        ### Add batch and head dimensions
        mask = jax.numpy.expand_dims(mask, 0)
        mask = jax.numpy.expand_dims(mask, 0)
        mask = jax.numpy.broadcast_to(mask, out_shape)
    mask = mask.astype(jax.numpy.bool_)
    return mask

def get_packing_mask(seq_ids, out_shape=None):
    # B x S x 1
    expand0 = jax.numpy.expand_dims(seq_ids, axis=2)
    # B x 1 x T
    expand1 = jax.numpy.expand_dims(seq_ids, axis=1)
    # B x S x T
    mask = ~jax.numpy.equal(expand0, expand1)
    if out_shape is not None:
        ### Add head dimension
        mask = jax.numpy.expand_dims(mask, 1)
        mask = jax.numpy.broadcast_to(mask, out_shape)
    mask = mask.astype(jax.numpy.bool_)
    return mask

@jax.jit
def attention_ourselves(_Q, _K, _V):
    _weights_unnormalized = jax.numpy.einsum("BSHD,BTHD->BHST", _Q, _K)
    _mask_causal = get_causal_mask(SEQUENCE, _weights_unnormalized.shape)
    _mask_packing = get_packing_mask(seq_ids, _weights_unnormalized.shape)
    _mask = jax.numpy.logical_or(_mask_causal, _mask_packing)
    _weights = jax.nn.softmax(_weights_unnormalized - 1e6*_mask)  
    output = jax.numpy.einsum("BHST,BTHD->BSHD", _weights, _V)

    return output

def attention_pallas(_Q, _K, _V):
    return pallas_attention.mha_reference(_Q, _K, _V,  segment_ids=seq_ids, causal=True)

attn_ourselves_non_sharded = attention_ourselves(Q_,K_,V_)
attn_ourselves_value = attention_ourselves(Q,K,V)
attn_value = attention_pallas(Q,K,V)

assert jax.numpy.allclose(attn_ourselves_value, attn_ourselves_non_sharded, atol=1e-1, rtol=1e-1)
assert jax.numpy.allclose(attn_ourselves_value, attn_value, atol=1e-1, rtol=1e-1)

time_ourselves_ns = simple_timeit(attention_ourselves, Q_, K_, V_, task="ourselves_ns")
time_ourselves = simple_timeit(attention_ourselves, Q, K, V, task="ourselves")   
time_pallas = simple_timeit(attention_pallas, Q, K, V, task="pallas")

"""
Output:

ourselves_ns: average time milliseconds: 8.68, trace /tmp/t_ourselves_ns_PBJJR6FUT8
ourselves: average time milliseconds: 2.33, trace /tmp/t_ourselves_W39992S9Z7
pallas: average time milliseconds: 2.78, trace /tmp/t_pallas_G8UDE4Y3EB
"""

Parallelization gives a speedup by 75% if we have our hands on 4 chips as each chip will process only 1/4 of the data instead of one chip all of it.

This blogpost is heavily influenced by the following course by Rafi Witten. The book of Bishop & Bishop was helpful as well. The experiments were supported by Googles TRC program.

You May Also Enjoy

Introduction to basic probability.

2 minute read

Let us start with the notion of a sample space. A sample space describes the set of all possible outcomes when performing an experiment.